דיאגרמת התפצלות

במתמטיקה, במיוחד במערכות דינמיות, דיאגרמת ביפורקציות (בעברית התפצלות) מציגה את הערכים שאליהם המערכת שואפת אסימפטוטית (שיכולים לכלול נקודות קבועות, מסלולים מחזוריים או אטרקטורים כאוטיים) כפונקציה של פרמטר כלשהו (הנקרא פרמטר בפירוקציה) של המערכת.^{[דרוש מקור]} נהוג לייצג ערכים יציבים עם קו מלא וערכים לא יציבים עם קו מקווקו, אם כי לעיתים קרובות הנקודות הלא יציבות מושמטות מהאיור. דיאגרמות התפצלות מאפשרות הדמיה של תורת הביפורקציה. בהקשר של מערכות דינמיות בזמן בדיד (דיסקרטי), הדיאגרמה נקראת גם דיאגרמת מסלול.

דיאגרמת התפצלות של המפה הלוגיסטית

דיאגרמת התפצלות של מפת המעגל. אזורים שחורים תואמים ללשונות ארנולד (תופעה שמתרחשת כאשר צופים במערכות דינמיות).

מפה לוגיסטית

דיאגרמת התפצלות של המפה הלוגיסטית. האטרקטור לכל ערך של פרמטר כלשהו r מוצג על הקו האנכי המתאים לערך הפרמטר r.

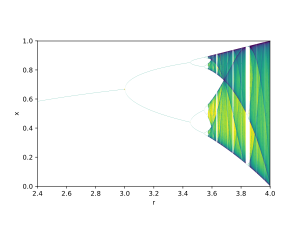
דוגמה לכך היא דיאגרמת הביפורקציה של המפה הלוגיסטית :

$$x_{n+1}=rx_{n}(1-x_{n}).$$

פרמטר הביפורקציה r מוצג על הציר האופקי של הגרף והציר האנכי מציג את קבוצת הערכים של הפונקציה הלוגיסטית מכל תנאי ההתחלה האפשריים.

דיאגרמת הביפורקציה מראה התפצלות של מסלולים יציבים לשני חלקים, ארבעה, שמונה, וכך הלאה. כל אחת מנקודות הביפורקציה האלו נקראת perioud doubling bifurcation. היחס בין האורכים של אינטרוולים של ביפורקציות עוקבות עבור מתכנס לקבוע שנקרא first Feigenbaum.

שבירת סימטריה במערכות הביפורקציה

שבירת סימטריה בהתפצלות קלשון כאשר הפרמטר ε משתנה. ε = 0 הוא המקרה של התפצלות קלשון סימטרית.

במערכת דינמית כגון

$${\ddot {x}}+f(x;\mu )+\varepsilon g(x)=0,$$

אשר יציבות מבחינה מבנית כאשר $\mu \neq 0$, אם משרטטים דיאגרמת ביפורקציה, ניתן להתייחס ל - $\mu$ כפרמטר הביפורקציה, עבור ערכים שונים של $\varepsilon$,. המקרה בו $\varepsilon =0$ נקרא התפצלות הקלשון הסימטרית. כאשר $\varepsilon \neq 0$, אנחנו אומרים שיש לנו קלשון עם סימטריה שבורה. זה מודגם באנימציה משמאל.

יישומים

בהינתן מערכת של משוואות דיפרנציאליות המתארות ערך פיזיקלי כלשהו. למשל המיקום והמהירות של מטוטלת חופשיה וללא חיכוך, פוטנציאל הממברנה של נוירון לאורך זמן, או הריכוז הממוצע של וירוס במחזור הדם של המטופל. המשוואות הדיפרנציאליות עבור הדוגמאות הללו כוללות *פרמטרים* שעשויים להשפיע על הפלט של המשוואות. למשל, שינוי המסה ואורכה של המטוטלת ישפיעו על תדירות התנודות שלה, שינוי גודל הזרם המוזרק לנוירון עשוי להעביר את פוטנציאל הממברנה ממנוחה לירי, והעומס הנגיפי לטווח ארוך בזרם הדם עשוי לרדת כתגובה לטיפול.

באופן כללי, חוקרים מעוניינים לכמת כיצד ההתנהגות ארוכת הטווח (האסימפטוטית) של מערכת של משוואות דיפרנציאליות משתנה אם פרמטר משתנה. בענף המתמטי של מערכות דינמיות, דיאגרמת ביפורקציה מכמתת את השינויים הללו על ידי חקירת נקודות השבת, המסלולים המחזוריים או האטרקטורים הכאוטיים של מערכת משתנים כפונקציה של פרמטר ביפורקציה. דיאגרמות התפצלות משמשות כדי לדמיין שינויים אלה.

ראו גם

• זיכרון התפצלות
• תורת הכאוס
• דיאגרמת שלד של התפצלות
• קבועי פייגנבאום

לקריאה נוספת

• Glendinning, Paul (1994). Stability, Instability and Chaos. Cambridge University Press. ISBN 0-521-41553-5.
• May, Robert M. (1976). "Simple mathematical models with very complicated dynamics". Nature. 261 (5560): 459–467. Bibcode:1976Natur.261..459M. doi:10.1038/261459a0. PMID 934280.
• Strogatz, Steven (2000). Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering. Perseus Books. ISBN 0-7382-0453-6.

קישורים חיצוניים

• המפה והכאוס הלוגיסטית מאת Elmer G. Wiens, egwald.ca
• Wikiversity: דיאגרמת מסלול מערכת דינמית בזמן דיסקרטי